Lo scopo di questo progetto è studiare e realizzare diversi metodi di interazione con curve N.U.R.B.S., che permettano al disegnatore una via semplice ed intuitiva per ottenere la forma della curva voluta.
Una curva N.U.R.B.S. è una generalizzazione delle curve B-Spline, verrà quindi brevemente introdotta la teoria che supporta la costruzione di questo genere di curve, per poi arrivare alla definizione di una N.U.R.B.S. vera e propria.
Le curve formate da un unico polinomio (Bèzier) non sono adatte per la costruzione di forme geometriche complesse,
per le quali è necessario un alto numero di vincoli e quindi un polinomio di grado molto elevato; infatti per interpolare n-punti
è necessario un polinomio di grado n-1, numericamente instabile a causa
della propagazione degli errori di troncamento.
Inoltre, modificando i punti di controllo, tutta la curva viene influenzata.
Per eliminare questi inconvenienti sono state introdotte delle curve polinomiali a tratti, definite da
dove {Pi} sono i punti di controllo (che vanno a formare "IL POLIGONO DI CONTROLLO") mentre {fi} sono funzioni polinomiali non nulle solo su una porzione limitata dell'intervallo di variazione del parametro {u} e nulle in tutto il resto dell' intervallo, garantendo così il "local support". In questo modo, variando la posizione di un control point, la curva verrà influenzata solo in un suo intorno.
Per calcolare le funzioni base di una curva B-Spline bisogna conoscere il grado {p} della curva e il vettore dei nodi {K}.
Dove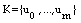 
è una sequenza di numeri reali detti nodi,
e dove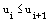 
con i=0, ... , i=m-1;
si definisce la "i-esima funzione di grado p", ovvero di ordine (p+1), indicata con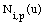 
,
come segue:
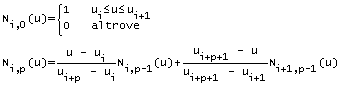
nella quale vengono evidenziati i seguenti importanti aspetti:
- per ogni p>0, {Ni,p(u)} è una combinazione lineare di due funzioni base di grado p-1;
- se nel calcolo delle funzioni base si determina un quoziente 0/0, viene definito uguale a zero;
- le funzioni di base sono ottenute per ricorsione sfruttando la formula di Cox-deBoor;
- i nodi possono coincidere, con la possibilità di avere dei sotto-intervalli di lunghezza nulla;
- le funzioni di base definite su un vettore dei nodi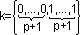 
generano dei polinomi di Bernstein di grado {p} e sono quindi le stesse funzioni di base di una curva
di Bèzier; in questo senso, quindi, le curve B-Spline sono generalizzazioni delle curve di Bèzier.
Una curva B-Spline di grado {p} è definita da :
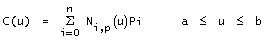
dove {Pi} sono i punti di controllo della curva, e {Ni,p(u)} sono le funzioni delle basi di curve B-Spline di grado "p", definite su un vettore "K" dei nodi non periodico e non uniforme:
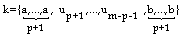
e viene calcolata utilizzando questo procedimento:
- si ricava l'intervallo di appartenenza del parametro {u};
- si calcolano le funzioni di base diverse da zero;
- si ricava la curva moltiplicando il valore delle funzioni di base non nulle per i punti di controllo;
Una successiva generalizzazione è servita per risolvere determinati problemi che si hanno con le curve B-Spline; il più significativo è dato dall' impossibilità di disegnare figure semplici come il cerchio. Mediante questa evoluzione è infatti possibile rappresentare correttamente curve coniche, ed è possibile rappresentare curve molto complesse con un minor numero di punti di controllo.
Le N.U.R.B.S. (Non Uniform Rational B-Spline), sono curve razionali definite da punti di controllo e dai relativi pesi;
aumentando il valore del peso di un punto di controllo avviciniamo la curva al punto stesso; viceversa il punto di controllo
eserciterà una minor influenza sulla curva.
Una curva N.U.R.B.S. di grado "p" è definita da :
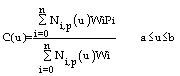
Dove {Pi} sono i punti di controllo della curva, {Wi} sono i pesi assegnati ad ogni punto di controllo e {Ni,p(u)} sono le funzioni delle basi di curve B-spline di grado "p" definite su un vettore "K" dei nodi non periodico e non uniforme:
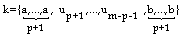
Se assumiamo che a = 0, b = 1 e che {Wi} > 0 per ogni i, possiamo definire
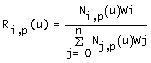
questo ci permette di riscrivere l'equazione che definisce una curva N.U.R.B.S. come
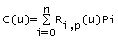
dove {Ri,p(u)} sono le funzioni razionali delle basi che sono pezzi di funzioni razionali su u appartenente [0,1].
Il tool di modifica realizzato in questo progetto, va ad agire sulle caratteristiche fondamentali di una curva N.U.R.B.S.
Sono stati sviluppati tre metodi per modificare la curva in maniera più intuitiva; questi metodi vanno
ad influire sulla posizione dei Punti di Controllo. Una volta identificato il punto della curva su cui si vuole agire,
vengono ricavati i Punti di Controllo che hanno influenza sullo stesso e si va a modificare la loro posizione contemporaneamente,
ottenendo così una deformazione della curva più dolce.
Il tool calcola anche la derivata prima della curva ( la derivata di una funzione base è definita
come combinazione lineare di due funzioni base di grado {p-1} ) fornendo così un idea più precisa
della pendenza della curva nel punto selezionato.
Analizzerò ora le tre tipologie del tool realizzato:
Per ottenere questa modifica si calcola il vettore spostamento subito dal puntatore del mouse, durante la modifica della curva, e si applica questa traslazione a un numero di Control Point pari al grado della curva. La traslazione viene pesata in base all'influenza che ogni singolo Control Point ha sul punto della curva selezionato. Quindi un Control Point con maggiore influenza sul punto, a parità del modulo del vettore generato, verrà traslato maggiormente rispetto a uno con influenza minore.
Per ottenere questa modifica si assegna allo spostamento verticale del mouse un angolo teta, si applica poi una matrice di rotazione, con angolo teta, a un numero di Control Point pari al grado della curva. La rotazione così ottenuta influenza la curva facendo ruotare i Control Point rispetto al punto della curva selezionato.
Al contrario del precedente tool di traslazione in questa modifica vengono interessati solo i due Control Point tra i quali il punto della curva selezionato è compreso. Si calcola il vettore generato dallo spostamento del mouse,ad esempio dal punto "a" al punto "b", che viene applicato al Control Point inferiore come vettore [b-a] (segue la traslazione del mouse) mentre al Control Point superiore come vettore[a-b] (opposto alla traslazione del mouse).
Per concludere la parte teorica è necessario chiarire come il tool vada ad agire sulla curva.
Una volta riempita la struttura dati N.U.R.B.S. con i parametri prima indicati, ed aver quindi ricavato tutti i suoi punti,
gli algoritmi non fanno altro che:
- Individuare su quale punto della curva l'utente vuole interagire;
- Valutare le basi non nulle e quindi quali Control Point vanno ad influire sul punto della curva;
- Individuare tra quali Control Point il punto selezionato è compreso;
- Applicare una delle tre trasformazioni indicate in precedenza ai Control Point marcati;
- Ricalcolare i punti della curva, e la sua derivata prima.
